carrucola fissa mobile composta

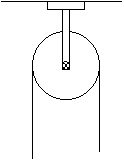
In meccanica una carrucola è una macchina molto semplice atta a sollevare pesi costituita da una ruota girevole attorno ad un perno fissato ad una staffa e recante alla periferia una scanalatura entro cui scorre un organo flessibile di trasmissione, come una fune, una cinghia, ecc. La carrucola si dice:

• fissa (vedi foto), se la staffa è attaccata ad un supporto fisso;

• mobile (vedi foto), quando il peso è attaccato alla staffa, che quindi sale e scende con esso;

• composta (vedi foto), se costituita da carrucole fisse e mobili.

Quando ad una carrucola semplice si sospendono due masse differenti, il sistema non può essere ovviamente in equilibrio, ma tende a far scendere la massa maggiore e a far salire quella minore con un'accelerazione inferiore a quella di gravità g = 9,806 m/s². Da un punto di vista qualitativo la massa inferiore frena nella sua caduta il moto di caduta libera della massa maggiore appesa all'altro estremo della fune. Quanto affermato può essere naturalmente dimostrato e l'impostazione delle semplici leggi della dinamica permette di pervenire anche ad esprimere l'accelerazione a con cui la massa maggiore scende al suolo in funzione delle due masse che caratterizzano il sistema, facendo l'ipotesi semplificativa che la carrucola sia ideale, ovvero con massa nulla (trascurabile).

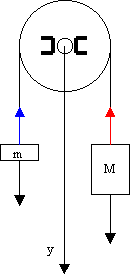
Con particolare riferimento al sistema nel disegno qui a lato, la prima equazione cardinale della dinamica per la massa m porta a scrivere che ma_m = -T + mg, ovvero che l'accelerazione a_m della massa m (positiva se verso il basso, cioè se concorde con l'asse delle y) è pari alla somma (vettoriale) della tensione T verso l'alto dovuta alla fune e alla forza peso mg ovviamente rivolta verso il basso. La prima equazione cardinale della dinamica scritta invece per la massa maggiore M assume l'espressione Ma_M = -T + mg, ovvero l'accelerazione a_M della massa M è pari alla somma (vettoriale) della tensione T dovuta alla fune e alla forza peso Mg.

Poiché le due masse sono unite tra loro per mezzo della fune (supposta inestensibile e con massa trascurabile), è evidente che si può scrivere l'uguaglianza a_M = -a_m ovvero che, in altre parole, le due masse M e m sono caratterizzate dalla stessa accelerazione con l'unica ovvia differenza che mentre una sale l'altra non può che necessariamente scendere. Inoltre, dato che si è supposta la carrucola ideale, ciò è sufficiente per affermare che le due tensioni sono uguali. A questo punto, per ottenere l'accelerazione della massa M, indicata semplicemente con a e rivolta verso il basso, non resta che eseguire delle semplici sostituzioni. L'espressione di a è a = g(M - m)/(M + m) [1], inferiore all'accelerazione di gravità, essendo M - m minore di M + m.

Un'osservazione è d'obbligo. Nella realtà la carrucola ideale non esiste e pertanto la sua puleggia ha una certa massa che impone di tener conto anche del suo momento d'inerzia I e ciò porta ad una leggera complicazione nella determinazione dell'espressione dell'accelerazione a di caduta della massa maggiore. Tralasciando i passaggi, l'applicazione delle equazioni cardinali della dinamica o, in alternativa, del principio di conservazione dell'energia meccanica, porta alla seguente espressione per l'accelerazione a della massa M: a = g(M - m)/(m + M + I/r²) [2], se con r si indica il raggio della ruota della puleggia. Tale accelerazione è ovviamente inferiore a quella di gravità e minore di quella ottenuta nel caso di carrucola ideale tramite l'equazione [1]. Si tenga poi presente che l'aggiunta degli attriti, sempre presenti, contribuisce a ridurre ancora il valore di a.

La macchina di Atwood sfrutta questo sistema per far avvenire moti di caduta "libera" di un grave con accelerazione inferiore a quella di gravità e pari a circa 1/33 di g nei modelli in cui M = 17/16 m, com'è facilmente ottenibile dalla relazione semplificata [1], ovvero assumendo trascurabile in prima approssimazione la massa della carrucola fissa presente nello strumento.