clindrica a imbuto tronco conica a T
Pressione trasmessa alle superfici di sostegno
| meccanica dei fluidi - liquidi | ||
|---|---|---|
| Supporto teorico | ||
| Paradosso idrostatico | ||
Il cosiddetto paradosso idrostatico consiste nel fatto che la forza esercitata da un fluido su un corpo solido in esso immerso non è proporzionale come sarebbe facile credere al volume del fluido, ma alla dimensione della superficie sotto pressione e all'altezza della massima colonna di fluido che la sovrasta. La formulazione di questa evidenza fisica che riguarda i fluidi in quiete è opera di B. Pascal, cui si deve anche l'enunciato del principio di Pascal (1583). In altre parole, la forza che tenderebbe a far saltare la flangia di chiusura a livello del fondo di un serbatorio è indipendente dalla forma dello stesso e dalla quantità di liquido, ma dipende solo dalla superficie della flangia e dall'altezza della colonna di liquido che la sovrasta. Così le flange esattamente dello stesso tipo poste sul fondo di serbatoi con forme diverse, differenti volumi dello stesso liquido, ma alla stessa profondità dal pelo libero, sono soggette alla stessa spinta, poiché la pressione su di esse è la stessa. Quanto appena detto sulla pressione discende dalla prima legge delle tre leggi della pressione nei fluidi incomprimibili e in quiete (legge idrostatica). Così un'altra possibile formulazione del paradosso idraulico è la seguente: la pressione in un punto qualsiasi di un liquido non dipende nè dalla sua quantità nè dalla forma del recipiente, ma solamente dalla profondità del punto dal pelo libero.
| Galleria d'immagini |

|
| Spinta sul fondo di un serbatoio di area A e forma clindrica a imbuto tronco conica a T Pressione trasmessa alle superfici di sostegno |
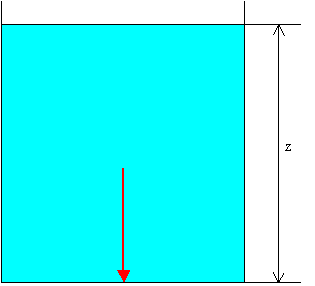
Da un punto di vista matematico la dimostrazione del paradosso idrostatico è assai semplice, dato che, per la legge idrostatica scritta in termini di pressione relativa, la pressione di un punto alla profondità z in un liquido di peso specifico γ è pari a p = γz. Considerando allora il fondo (disposto orizzontalmente) di un recipiente di area totale A, la forza infinitesima che il fluido esercita su una sua porzione dA è pari a dF = pdA = γzdA. Essendo la superficie orizzontale, essa è una superficie isobara per la terza legge delle tre leggi della pressione nei liquidi. Ne segue che p è costante sul fondo del recipiente in esame, dato che sia z che γ non cambiano. Allora la forza totale F che sollecita il fondo del serbatoio non è altro che la somma (integrale) estesa su tutta l'area A di tanti termini infinitesimi tutti uguali e pertanto F = γzA, indipendente dalla massa del fluido e dalla forma del recipiente. Il termine γz esperime proprio la colonna di liquido che grava sul fondo.
Il paradosso idrostatico fu chiarito da Stevino nel 1586 in base al cosiddetto "principio di solidificazione". Si consideri infatti un serbatoio cilindrico di area A. La spinta F (in rosso) sul fondo sarà pari a F = γzA. Nel caso di un serbatoio a imbuto con la stessa area di fondo la parte liquida tratteggiata può considerarsi sostituita da una sostanza solida avente il medesimo peso specifico del liquido senza alterare l'equilibrio delle forze. Invece con un serbatoio tronco conico sempre della stessa area di base A, può essere sostituita con lo stesso liquido presente all'interno del contenitore tutta la parte in colore azzurro più chiaro senza che ciò modifichi la spinta F e analogo discorso vale per il serbatoio a T, anch'esso con la stessa area di base degli altri. Ciò che conta infatti è, a parità d'area di base, l'altezza z della colonna di fluido sovrastante.
Da quanto detto emerge il fatto che anche una piccola quantità di liquido è in grado di generare pressioni idrostatiche notevoli. Ciò fu provato da Pascal per mezzo di un esperimento assai semplice, ma di notevole effetto. Riempita d'acqua una botte perfettamente integra e in ottimo stato, egli fissò molto bene ad essa un tubo di piccolo diamatro in verticale che poi fu riempito anch'esso con acqua. Le cronache riportano che Pascal con una semplice colonna d'acqua di 10 metri d'altezza riuscì a sfasciare la botte. Il perchè è evidente: la situazione è simile a quella del contenitore a T. La pressione a livello della base della botte è proporzionale all'altezza z della colonna d'acqua ed essa non è certo costruita per reggere questa pressione.
E' importante sottolineare che la pressione idrostatica sul fondo di un contenitore non va confusa con quella che il recipiente esercita sui corpi che lo sostengono. Quest'ultima è infatti sempre uguale al peso totale del sistema (ovvero del peso del vaso più quello del liquido che esso contiene) diviso per l'area d'appoggio, mentre la prima può essere maggiore, minore o uguale della seconda in base alla forma del contenitore. Anche questa affermazione sembra in un primo momento paradossale, ma per venirne a capo si immagini allora un contenitore (vedi figura) formato dall'unione di due serbatoi cilindrici con aree diverse pieno d'acqua fino all'orlo. Il fondo sopporta la pressione p = γz, con z l'altezza totale dal liquido dal fondo, e tale pressione è la stessa che si misurerebbe se il diametro del recipiente fosse in tutta la sua altezza uguale a quello della base. Si sarebbe allora tentati a concludere che, mettendo il sistema sul piatto di una bilancia, la forza che il sistema trasmette ad esso sia pari al peso che darebbe un contenitore riempito d'acqua fino alla stessa altezza e con diametro pari a quello di base del contenitore reale. Tuttavia ciò non è vero, dal momento che la pressione idrostatica agente sul fondo del contenitore non si trasmette integralmente su piatto della bilancia. Infatti all'interno del vaso in corrispondenza della superficie superiore del recipinete più ampio si ha una pressione rivolta dal basso verso l'alto (indicata dalle frecce nere in figura). Ciò ha come effetto la riduzione della pressione che si trasmette al piatto della bilancia ed è facile verificare che il valore di pressione trasmesso è proprio pari a quella data dalla somma del peso del contenitore con quello del fluido.