
REGISTRO VISITATORI
| TA KIMIKA - Laboratorio | |
|---|---|
 REGISTRO VISITATORI |
Elementi di statistica |
| La media | |
| Precedente - Pagina - Successiva | |
La media <x> è un indice di posizione centrale e viene utilizzata, quando significativa, come valore di sintesi ovvero come un valore che riassume una caratteristica di un insieme di dati (campione). Non sempre la media è in grado di "sintetizzare" un campione; quando lo è, la media offre una stima della tendenza dei valori a un valore centrale.
Di medie ce ne sono più di una. Qui non le tratteremo tutte, ma solo due: la media aritmetica e la media aritmetica ponderata. Si immagini allora di avere un campione di N elementi x1, x2, x3, ..., xi, ..., xN. Ecco come queste due medie sono definite e calcolate.
Media aritmetica - E' definita come la somma Σ di tutti gli N valori del campione, cioè il primo valore (i = 1) più il secondo (i = 2) più il terzo (i = 3) ... più l'ennesimo (i= N) diviso il numero complessivo degli elementi del campione (qui N). In formule
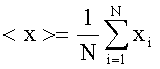
La media aritmetica, oltre ad essere la più semplice tra le varie medie, ha la caratteristica di trattare tutti i valori del campione allo stesso modo ovvero nessun elemento è più importate, ha più "peso" degli altri. Quando invece in un campione certi elementi pesano di più di altri, la media aritmetica non è quella giusta per rappresentarlo.
Media aritmetica ponderata - Vediamo un classico caso di impiego di questa particolare media. Dallo studio della chimica si sa che gli atomi degli elementi non sono tutti rigorosamente uguali, a causa degli isotopi. Per esempio gli atomi che formano il gas cloro (Cl2) hanno tutti 17 protoni, ma non lo stesso numero di neutroni. Infatti vi possono essere atomi di cloro con 18 neutroni (massa 34,97 u.m.a.) e atomi con 20 neutroni (massa 36,97 u.m.a.). Se per ogni atomo con 18 neutroni ce ne fosse uno con 20, il peso atomico medio dell'atomo di cloro sarebbe dato dalla media aritmetica tra la massa atomica dei due isotopi, ma in realtà su 100 atomi di cloro mediamente 75,77 sono di isotopo 35Cl e 24,23 sono atomi di cloro con 20 neutroni nel nucleo. Le masse atomiche dei due isotopi hanno evidentemente un contributo (in gergo statistico di dice "peso") diverso nel produrre la massa atomica media dell'atomo di cloro.
Dunque nel calcolo della massa media dell'atomo di cloro si deve valutare il peso di ogni singolo isotopo e tale contributo è quantificato dalla sua abbondanza percentuale. Quando nell'operazione di media i valori sono moltiplicati per un coefficiente ponderale, si ha la media ponderata. Così la massa atomica media di ciascun elemento è calcolata effettuando la sommatoria tra tutte le masse atomiche di ogni isotopo ciacuna moltiplicata per la relativa abbondanza percentuale. Si osservi che la somma dei pesi è in questo caso pari a 100, cosicché nei calcoli che seguono si è direttamente proceduto a dividere per 100 tutte le percentuali.
In termini numerici, per il cloro MCl = 34,97x0,7577 + 36,97x0,2423 = 35,45 u.m.a. Analogamente per l'ossigeno (che si presenta in natura con 3 isotopi: 16O - 15,9949 u.m.a. 99,759%, 17O - 16,9991 u.m.a. 0,037%, 18O - 17,9991 u.m.a. 0,04%) MO = 15,9949x0,99759 + 16,9991x0,00037 + 17,9991x0,0004 = 15,994 u.m.a. Si vede chiaramente che il maggior contributo è dell'isotopo 16: non avrebbe avuto senso attibuire lo stesso contributo agli altri due isotopi assai meno abbondanti.
Da un punto di vista generale, indicato con pi il peso associato al dato xi, la media aritmetica pondrata <xp> si calcola come quoziente fra la somma dei prodotti dei dati per i loro pesi e la somma dei pesi stessi; in formule:
x1p1 + x2p2 + ... + xNpN
<xp> = ---------------------------
p1 + p2 + ... + pN
Qualora un insegnante decidesse che per formare il voto in pagella contano di più l'ultimo scritto e l'ultima interrogazione orale di ciascun qudrimestre, è evidente che in questo caso il rendimento di ogni alunno viene calcolato attraverso una media aritmetica ponderata sulla base di pesi opportuni dati a ciascuna verifica.
| Ultimo aggiornamento il |