

| acustica - Figure di Lissajous |
|---|---|
| Supporto teorico | |
| Curiosità sulle figure di Lissajous | |
| Figure di Lissajous tridimensionali |
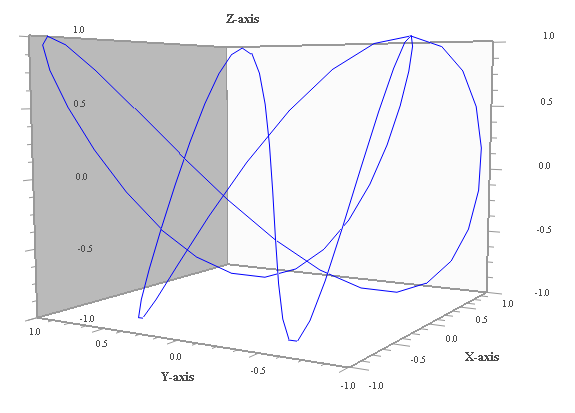 Esistono le figure di Lissajous in 3D, ovvero come curve dello spazio? La domanda è più che legittima. E probabilmente la risposta è scontata: sì, ci sono le curve di Lissajous tridimensionali, che a volte hanno un certo che di fascino artistico, soprattutto se disegnate con particolari effetti grafici... Poiché però l'argomento esula dai contenuti del Museo Virtuale di Fisica, qui se ne fa solamente un rapidissimo accenno.
Esistono le figure di Lissajous in 3D, ovvero come curve dello spazio? La domanda è più che legittima. E probabilmente la risposta è scontata: sì, ci sono le curve di Lissajous tridimensionali, che a volte hanno un certo che di fascino artistico, soprattutto se disegnate con particolari effetti grafici... Poiché però l'argomento esula dai contenuti del Museo Virtuale di Fisica, qui se ne fa solamente un rapidissimo accenno.
Estendendo le equazioni parametriche delle figure di Lissajous al caso spaziale, le equazioni assumono la seguente forma generale (adottando per esempio la funzione coseno)
x = A1cos(ω1t+φ1) y = A2cos(ω2t+φ2) z = A3cos(ω3t+φ3)
in cui A1, A2 e A3 sono le ampiezze di oscillazione, ω1, ω2 e ω3 le pulsazioni (legate alla frequenza) e φ1, φ2 e φ3 le fasi. Il moto complessivo risulta essere la composizione di tre moti pendolari reciprocamente ortogonali. Analogamente al caso bidimensionale (più facile da trattare anche in termini di generazione delle varie figure), per avere una curva periodica i rapporti tra le pulsazioni devono essere dei numeri razionali. In ogni caso la curva è contenuta nel parallelepipedo di lati 2A1, 2A2 e 2A3.
Curiosità: una figura di Lissajous bidimensionale è considerabile come il frutto della proiezione ortogonale su di un piano di una curva tridimensionale. Infatti, osservando a una certa distanza il parallelepipedo che contiene la curva tridimensionale per esempio ortogonalmente a una faccia della superficie laterale, chiaramente si perde una dimensione e si ha una delle curve bidimensionali di Lissajous appartenenti alla famiglia del particolare rapporto tra le pulsazioni "superstiti". La stessa cosa accade osservando la curva perpendicolarmente a una delle basi del parallelepipedo di contenimento e chiaramente qui viene a perdersi il contributo della coordinata z.
Gli esempi che seguono dimostrano empiricamente quanto detto. Tutti sono ricavati con A1 = A2 = A3 = 1 e φ1 = φ3 = 0 per semplicità.
| Curva tridimensiuonale 1 ω1 = 1, ω2 = 1, ω3 = 1, φ2 = 45º |
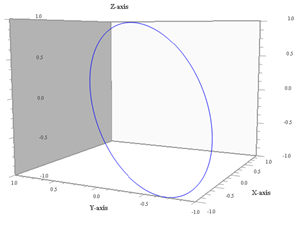
Curva tridimensiuonale 2 ω1 = 3, ω2 = 2, ω3 = 1, φ2 = 0º |
|---|---|
 |
 |
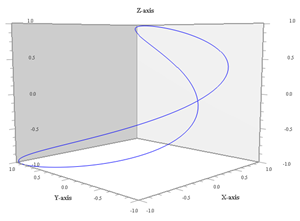
 Proiezione sul piano xz (ω2 non conta più) |
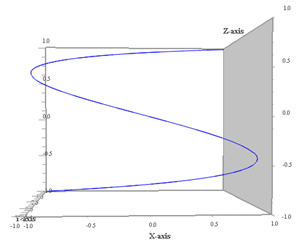 Proiezione sul piano xz (ω2 non conta più) |
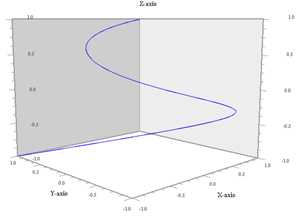
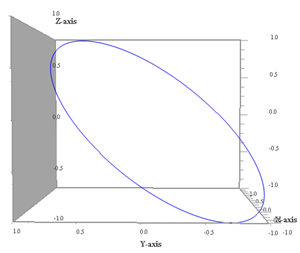 Proiezione sul piano yz (ω1 non conta più) |
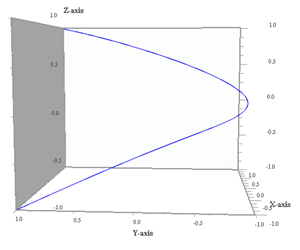 Proiezione sul piano yz (ω1 non conta più) |
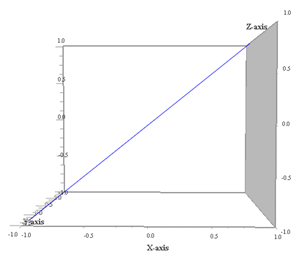
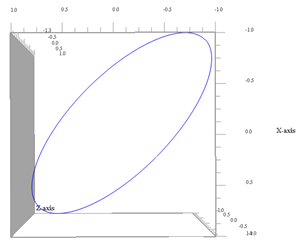 Proiezione sul piano xy (ω3 non conta più) |
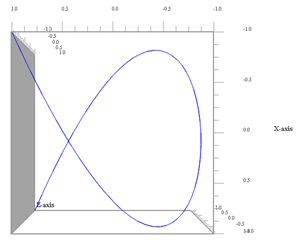 Proiezione sul piano xy (ω3 non conta più) |
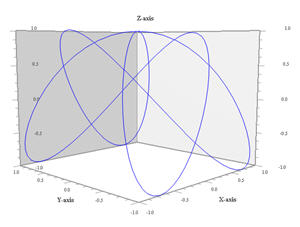
| Curva tridimensiuonale 3 ω1 = 1, ω2 = 2, ω3 = 1, φ2 = 30º |
Curva tridimensiuonale 4 ω1 = 3, ω2 = 2, ω3 = 4, φ2 = 90º |
 |
 |
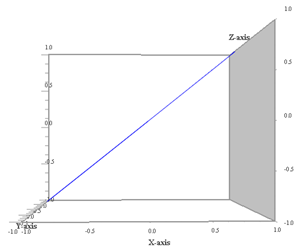 Proiezione sul piano xz (ω2 non conta più) |
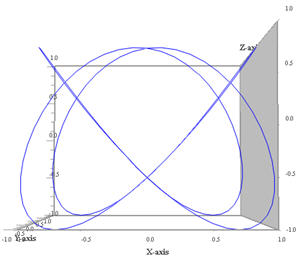 Proiezione sul piano xz (ω2 non conta più) |
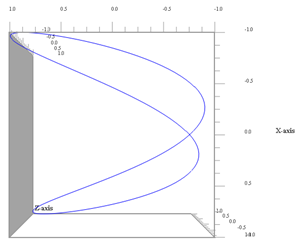
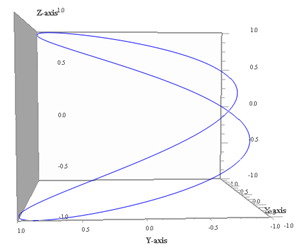 Proiezione sul piano yz (ω1 non conta più) |
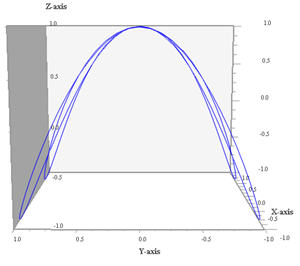 Proiezione sul piano yz (ω1 non conta più) |
 Proiezione sul piano xy (ω3 non conta più) |
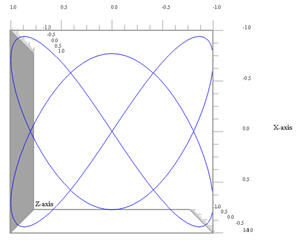 Proiezione sul piano xy (ω3 non conta più) |