 Facendo uso di un oscilloscopio, il cui visore è anche interpretabile come un piano cartesiano, con opportuni collegamenti si fa in modo che il primo segnale sinusoidale regoli l'andamento temporale delle x, mentre il secondo influenzi le y.
Facendo uso di un oscilloscopio, il cui visore è anche interpretabile come un piano cartesiano, con opportuni collegamenti si fa in modo che il primo segnale sinusoidale regoli l'andamento temporale delle x, mentre il secondo influenzi le y.| acustica - Figure di Lissajous - Applicazioni | |
|---|---|
| Supporto teorico | |
| Applicazioni delle figure di Lissajous | |
| Deduzione della rapporto tra le frequenze di due segnali elettrici |
 Facendo uso di un oscilloscopio, il cui visore è anche interpretabile come un piano cartesiano, con opportuni collegamenti si fa in modo che il primo segnale sinusoidale regoli l'andamento temporale delle x, mentre il secondo influenzi le y.
Facendo uso di un oscilloscopio, il cui visore è anche interpretabile come un piano cartesiano, con opportuni collegamenti si fa in modo che il primo segnale sinusoidale regoli l'andamento temporale delle x, mentre il secondo influenzi le y.
La composizione ortogonale di tali segnali fa quindi muovere nel piano cartesiano il punto P(x,y). Chiaramente si saranno regolate le scale degli assi cartesiani di modo che il punto P sia sempre contenuto entro il visore dell'oscilloscopio.
Ora, per quanto detto a commento della generazione interattiva di figure di Lissajous, se il rapporto tra le frequenze (ovvero tra le pulsazioni ω, essendo ω = 2πν, con ν = frequenza) è un numero irrazionale, l'osservazione nel tempo del movimento del punto P sul visore dello strumento dà luogo a una curva complessa ma non periodica.
Questa è per esempio la situazione che si presenta quando il secondo segnale viene modificato in frequenza direttamente dallo sperimentatore nella fase iniziale di un esperimento nel quale le frequenze devono invece possedere un preciso rapporto razionale, anche unitario.
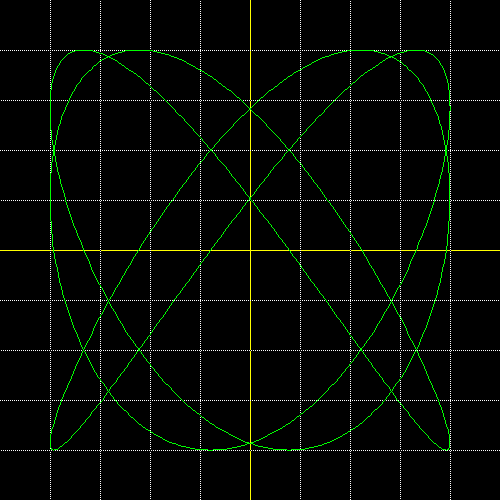
La comparsa sul monitor di una figura di Lissajous (ovvero di una curva periodica), consente di ricavare immediatamente il rapporto tra le frequenze dei due segnali, chiaramente note che siano le famiglie più significative di curve di Lissajous. Ad esempio, se apparisse la figura in questa pagina, si avrebbe l'immediata informazione che il rapporto tra le frequenze dei due segnali è 3/4, poiché si conoscono gli ingressi (quale è il segnale delle x e quello delle y). Se la figura fosse risultata ruotata di 90 º, allora il rapporto tra le pulsazioni sarebbe stato 4/3.
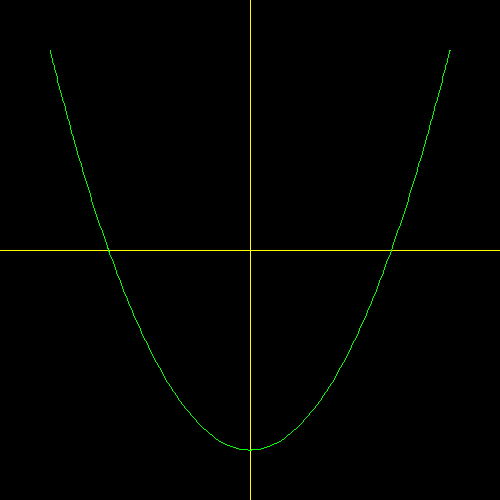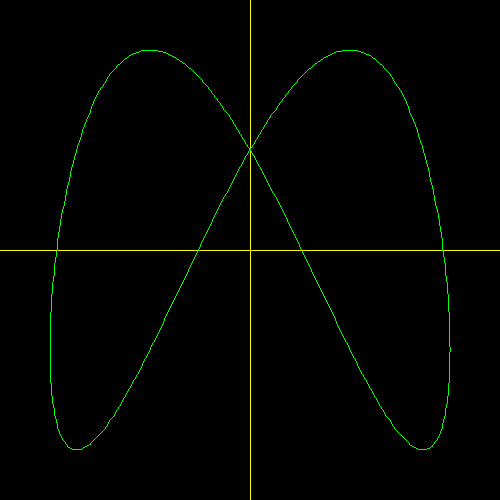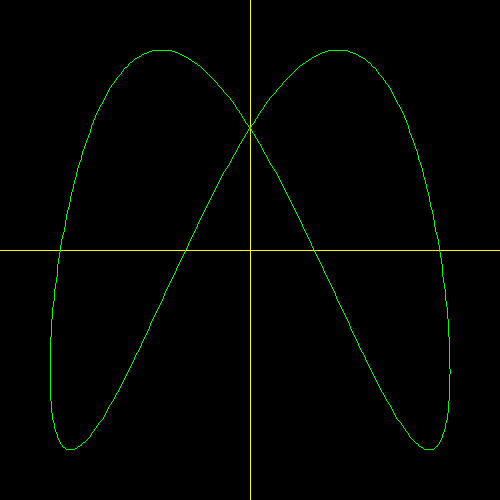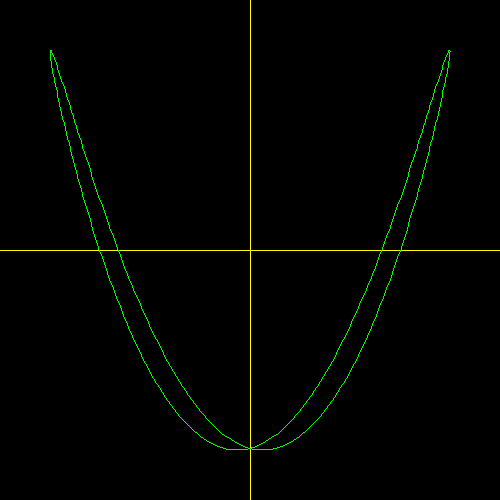 Il mantenersi costante nel tempo della figura di Lissajous prodotta sullo schermo dell'oscilloscopio testimonia la costanza della differenza di fase φ tra i due segnali in esame. Tuttavia questa condizione può anche non realizzarsi.
Il mantenersi costante nel tempo della figura di Lissajous prodotta sullo schermo dell'oscilloscopio testimonia la costanza della differenza di fase φ tra i due segnali in esame. Tuttavia questa condizione può anche non realizzarsi.
Nel caso in cui il rapporto tra le frequenze rimanga costante e sia invece presente nel tempo una variazione di fase φ fra i due segnali, la relativa figura di Lissajous visualizzata sullo schermo dell'oscilloscopio manifesterebbe delle progressive mutazioni di forma. Ma ognuna di tali figure mutevoli apparterrebbe alla famiglia generata dal particolare rapporto tra le pulsazioni dei due segnali che, per quanto assunto, non varia nel tempo.
Si immagini per esempio che i due segnali sinusoidali analizzati con l'oscilloscopio abbiano pulsazione uno doppia di quello dell'altro (cioè rapporto ω1/ω2 = 1/2) e che la fase φ cresca ciclicamente (ovvero da 0º cresca fino a 360º=0º e così di seguito). Ecco cosa si vedrebbe sullo schermo dell'oscilloscopio.