|
| acustica - Figure di Lissajous - Applicazioni |
|---|
| Supporto teorico |
|---|
| Applicazioni delle figure di Lissajous |
|---|
| Verifica della rapporto tra le frequenze di due segnali elettrici |
|---|
| Caso pari frequenza e fase costante |
|---|
 Si immagini che un dispositivo elettronico, quando in perfetta efficienza (ad esempio un filtro), elabori un segnale sinusoidale in ingresso in modo tale da produrre un segnale in uscita con identica frequenza (ovvero stessa pulsazione ω, visto che ω = 2πν, con ν = frequenza) e in aggiunta con differenza di fase φ costante. Come verificare che tale dispositivo funzioni come voluto?
Si immagini che un dispositivo elettronico, quando in perfetta efficienza (ad esempio un filtro), elabori un segnale sinusoidale in ingresso in modo tale da produrre un segnale in uscita con identica frequenza (ovvero stessa pulsazione ω, visto che ω = 2πν, con ν = frequenza) e in aggiunta con differenza di fase φ costante. Come verificare che tale dispositivo funzioni come voluto?
Facendo uso di un oscilloscopio e delle figure di Lissajous. Il visore di un oscilloscopio è anche immaginabile come piano cartesiano, quello che serve per osservare il muoversi di un punto P(x,y) tale per cui il segnale sinusoidale d'ingesso regoli l'andamento temporale delle y, mentre il segnale d'uscita influenzi le x. Ne segue che la composizione ortogonale di tali segnali fa muovere nel piano cartesiano il punto P(x,y). Chiaramente si dovranno regolate le scale degli assi cartesiani di modo che il punto P sia sempre contenuto entro il visore dell'oscilloscopio.
Ora, per quanto detto a commento della generazione interattiva di figure di Lissajous, se il rapporto tra le frequenze dev'essere unitario, l'osservazione nel tempo del movimento del punto P sul visore dello strumento deve necessariamente dare luogo a una figura di Lissajous:
1) stabile nel tempo (costanza di φ) e
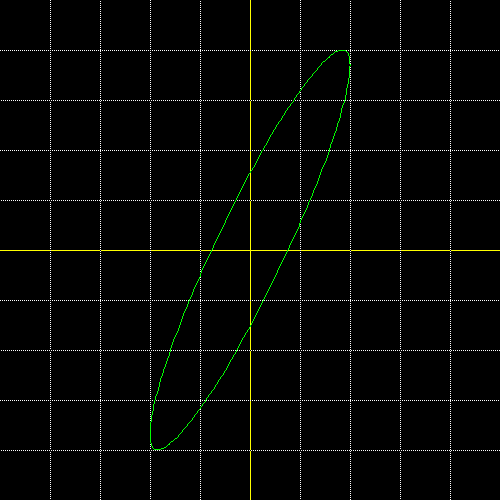
2) appartenente alla famiglia di curve con ω1/ω2 = 1 (segmento passante per l'origine degli assi, un'ellisse o un cerchio)
come per esempio quella rappresentata in figura.
Se ciò si verifica sperimentalmente, il dispositivo funziona correttamente e può essere utilizzato. Per di più, grazie a questa prova, si possono misurare i parametri caratterisitici dei due segnali per la frequenza ν utilizzata in ingresso. Assegnando per semplicità al lato dei quadrati dello schermo dell'oscilloscopio valore unitario, le coordinate (x,y) corrispondenti al vertice V dell'ellisse nel I quadrante sono V(2,4) circa. Ma per quanto detto y = 4 è l'ampiezza del segnale di ingresso, mentre x = 2 è la misura dell'ampiezza del segnale in uscita. Ne segue che, essendo ampiezza uscita/ampiezza ingresso = 2/4 = 0,5, il dispositivo elettrico in esame alla frequenza di lavoro ν riduce della metà l'ampiezza del segnale d'ingresso, cioè Auscita = 0,5Aingresso.
Anche il valore di φ può calcolato da misurazioni sullo schermo dell'oscilloscopio. Se si indica con B il punto di incontro dell'ellisse con il sempiasse positivo delle y (nell'esempio B = 1,7 circa, allora φ = arccos(B/Au), se Au è la misura dell'ampiezza del segnale d'uscita (qui Au = 2 circa). Nel caso si ottenesse un cerchio o un'ellisse con assi coincidenti con quelli coordinati o un segmento, non serve effettuare la misurazione, poiché per questi casi particolari la fase φ è nota.
 Si immagini che un dispositivo elettronico, quando in perfetta efficienza (ad esempio un filtro), elabori un segnale sinusoidale in ingresso in modo tale da produrre un segnale in uscita con identica frequenza (ovvero stessa pulsazione ω, visto che ω = 2πν, con ν = frequenza) e in aggiunta con differenza di fase φ costante. Come verificare che tale dispositivo funzioni come voluto?
Si immagini che un dispositivo elettronico, quando in perfetta efficienza (ad esempio un filtro), elabori un segnale sinusoidale in ingresso in modo tale da produrre un segnale in uscita con identica frequenza (ovvero stessa pulsazione ω, visto che ω = 2πν, con ν = frequenza) e in aggiunta con differenza di fase φ costante. Come verificare che tale dispositivo funzioni come voluto?