
| Meccanica - il giroscopio - giroscopi | ||
|---|---|---|

|
Supporto teorico | |
| Proprietà principali del giroscopio | ||
| Tenecia e precessione | ||
Non è qui il caso di dare prova in termini di formule matematiche delle due proprietà del giroscopio qui di seguito illustrate. Infatti, anche se il sistema dinamico può essere semplificato ricorrendo ad opportune ipotesi, il problema resta pur sempre complesso e al di fuori dei limiti di difficoltà stabiliti per le pagine del Museo Virtuale di Fisica.
Tenacia del giroscopio
In condizioni di quiete del corpo rotante (giroscopio) è possibile ruotarne l'asse giroscopico con una certa facilità. Basta applicare una forza sufficiente a vincere gli attriti a livello degli snodi del telaio. Tuttavia si osserva che la forza richiesta per effettuare la stessa operazione risuta essere decisamente maggiore nel caso in cui il corpo sia in rapida rotazione. L'intesità di tale forza risulta poi proporzionale alla velocità di rotazione.
Questa notevole inerzia dell'asse giroscopico e la sua capacità quindi di conservare immutata la direzione di rotazione è sfruttata in molteplici applicazioni pratiche: si va dalla guida e stabilizzazione dei satelliti artificiali, dei proiettili delle armi da fuoco, dei missili balistici e delle navi contro il rollio e il beccheggio alle girobussole (non influenzate dalla presenza di masse magnetiche nelle vicinanze). Non si dimentichi poi che una bicicletta in corsa sta in equilibrio proprio grazie alle ruote che sono a tutti gli effetti dei giroscopi.
Precessione del giroscopio (effetto giroscopico)
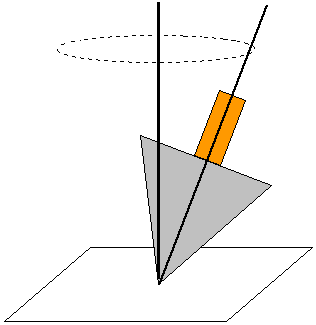 Per capire il comportamento del giroscopio si deve prima di tutto definire che cosa si intenda per moto di precessione. Si può dire, semplificando al massimo e sacrificando la precisione fisica, che un tipico moto di precessione è quello manifestato da una trottola, oggetto questo ben conosciuto.
Per capire il comportamento del giroscopio si deve prima di tutto definire che cosa si intenda per moto di precessione. Si può dire, semplificando al massimo e sacrificando la precisione fisica, che un tipico moto di precessione è quello manifestato da una trottola, oggetto questo ben conosciuto.
A rigore, si definisce invece moto di precessione quello manifestato da un corpo in rotazione attorno ad un asse (detto asse dei figura) e in cui tale asse ruota a sua volta attorno ad un asse diverso, detto asse di precessione. Un simile moto è causato della presenza sul sistema di un momento meccanico esterno. Per visualizzare meglio le cose, nel moto di una trottola l'asse di figura è quello di rotazione del corpo, mentre l'asse di precessione risulta essere perpendicolare al suolo ed è quello intorno al quale ruota il baricentro della trottola (e con esso il suo asse di figura).
Nel moto di precessione è importante individuare un punto particolare, il cosiddetto punto fisso Ω: esso è dato dall'intersezione dell'asse di precessione con quello di figura ed è l'unico punto del sistema che non ruota attorno all'asse di precessione. Rispetto a questo punto, che può coincidere o meno con il baricentro G del giroscopio, il risultante delle forze esterne applicate al sistema ha momento non nullo ed è proprio tale momento esterno che innesca il moto di precessione. Nella trottola il punto Ω è quello d'appoggio al suolo e la forza esterna (dal momento non nullo rispetto al punto fisso) è la forza peso.
La forza esterna, invece di rovesciare il corpo (come si è tentati a ipotizzare nel caso concreto della trottola), tende invece a far ruotare l'asse di figura con verso tale da portarlo parallelamente al verso del vettore che rappresenta il momento esterno applicato al giroscopio. Per questo motivo tale proprietà del giroscopio è detta anche "tendenza al parallelismo".
Per completezza si osserva che le ipotesi sotto le quali l'asse di un giroscopio resta immobile nel tempo in assenza di momenti esterni è verificata in un sistema inerziale. Sulla terra, che non è un sistema inerziale a causa della rotazione del nostro pianeta, un giroscopio in rapida rotazione lasciato indisturbato presenta un moto di rotazione dell'asse con verso opposto a quello di rotazione della terra. Inoltre è assai difficile che l'asse giroscopico sia anche asse principale d'inerzia per il corpo. Allora, in presenza di un momento esterno non nullo, al moto di precessione si aggiunge un'oscillazione dell'asse di figura. Il fenomeno si chiama nutazione.