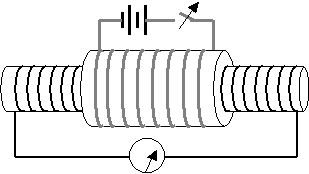
Si consideri il sistema in figura. Si tratta di due solenoidi di filo conduttore di diversa lunghezza e numero N di spire con nuclei caratterizzati da una certa permeabilità magnetica m (potrebbe trattarsi anche del vuoto o dell'aria). Il circuito sia isolato magneticamente da altre sorgenti esterne di campo magnetico.

Trascurando per il momento quele dei due circuiti sia collegato alla batteria e quele al galvanometro, il campo magnetico prodotto da uno dei due circuiti percorso da una certa corrente elettrica determina un flusso concatenato F_1,2 con qualsiasi altro circuito presente nella zona in cui agisce il campo magnetico di cui il primo circuio è sorgente. Analogo discorso vale per il secondo circuito: esso produrrà un flusso concatenato F_2,1 con il primo circuito. Si può dimostrare che valgono le relazioni di proporzionalità F_1,2 = Mi₁ e F_2,1 = Mi₂. Il termine M si chiama coefficiente di mutua induzione e ingloba tutti i fattori geometrici (forma e posizione relativa) e la dipendenza dal mezzo.

Si può inoltre dimostrare che, detti L₁ e L₂ i coefficienti di autoinduzione dei circuiti, M = K(L₁L₂)^0,5. Il termine K viene chiamato fattore di accoppiamento e il suo valore assoluto è sempre minore di uno.

Per il circuito in figura il coefficiente di mutua induzione è M = mn₁n₂S₁, se n₁ e n₂ sono il numero di spire per unità di lunghezza ed S₁ la sezione del nucleo più piccolo di permebilità magnetica m.