
Note sul copyright
Pagina Facebook
Firma anche tu il
REGISTRO VISITATORI
(GUEST BOOK)
 Note sul copyright Pagina Facebook Firma anche tu il REGISTRO VISITATORI (GUEST BOOK) | Elettromagnetismo - Elettrodinamica |
|---|---|
| Supporto teorico | |
| Concetto di flusso Φ |
Per la trattazione di alcuni problemi fisici è assai utile il concetto di flusso di un vettore e, in particolare, del flusso del campo elettrico, gravitazionale e di quello magnetico attraverso una superficie di area S. Il termine flusso ha una chiara origine idraulica.
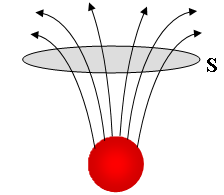 Si immaginino materializzate in una regione di spazio in cui è presente un campo di tipo vettoriale (campo elettrico, magnetico, gravitazionale) un certo numero di linee di forza e una superficie S attraversata da esse. Si può pensare a delle linee di forza che "sgorgano" dalla sorgente del campo andando ad attraversare la superficie S rispetto alla quale si intende calcolare il flusso.
Si immaginino materializzate in una regione di spazio in cui è presente un campo di tipo vettoriale (campo elettrico, magnetico, gravitazionale) un certo numero di linee di forza e una superficie S attraversata da esse. Si può pensare a delle linee di forza che "sgorgano" dalla sorgente del campo andando ad attraversare la superficie S rispetto alla quale si intende calcolare il flusso.
Se le linee di forza che attraversano S fossero tutte parallele tra loro e su S i vettori del campo tutti di pari intensità (cioè se il campo vettoriale fosse costante), allora come il volume di fluido che attraversa nell'unità di tempo la sezione S pensata come parte di una conduttura rappresenta la portata (m3/s), così il prodotto dell'area S per il modulo del campo vettoriale (qui infatti i vettori sono tutti uguali) rappresenta il flusso di tale campo attraverso tale superficie. In fisica è consuetudine indicare il flusso con la lettera graca Φ (fi maiuscola).
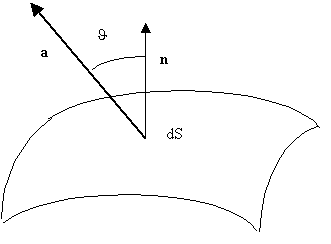 E se la superficie S non è piana e il campo è variabile nello spazio (cioè punto per punto su S i vettori sono diversi sia per modulo che per verso, per esempio come nel disegno), come si determina il flusso attraverso S? In generale infatti le linee di forza non tagliano perpendicolarmente la superficie S (oltre a variare punto per punto).
E se la superficie S non è piana e il campo è variabile nello spazio (cioè punto per punto su S i vettori sono diversi sia per modulo che per verso, per esempio come nel disegno), come si determina il flusso attraverso S? In generale infatti le linee di forza non tagliano perpendicolarmente la superficie S (oltre a variare punto per punto).
Il modo di procedere è il seguente. Si parte dal calcolo del flusso (infinitesimo) dΦ del vettore a attraverso una superficie infinitesima dS. Esso è matematicamente definito come dΦ = a • ndS, ovvero è pari al prodotto dell'area infinitesima dS per il prodotto scalare del vettore a che attraversa dS e la normale n (vettore di modulo unitario e perpendicolare alla superficie infinitesima dS).
Si ricorda che per le proprietà del prodotto scalare si ha che dΦ = acosθ. Da ciò si ottiene che il flusso infinitesimo dΦ è massimo quando a è parallelo a n (cioè quando a è perpendicolare a dS), nullo quando a è parallelo alla superficie dS (cos90º = 0).
Se allora si considera la generica superficie S formata da un mosaico di superfici infinitesime dS, il flusso Φ si ottiene sommando tutti i contributi infinitesimi dΦ (ovvero integrando sulla superficie S). Si sottolinea ancora una volta che in generale su S risultano variare sia il modulo del vettore a che la sua orientazione rispetto alla normale (ovvero varia θ).
In fine si fa notare che se per una causa qualsiasi dovessero modificarsi le linee di forza che attraversano una certa superficie S (perché la sorgente del campo si muove o perché è la superficie S a spostarsi o ancora perchè muta l'intensità del campo vettoriale), il flusso Φ attraverso la superficie S risulta variare nel tempo. Quest'ultima situazione è della massima importanza per spiegare il fenomeno dell'induzione elettromagnetica.
| La riproduzione totale o parziale di questa pagina e/o di sue parti con qualsiasi mezzo è consentita solo se è senza fini di lucro e sempre con la citazione ben visibile su tutti gli oggetti del nome o dei nomi degli autori e del Liceo Marco Foscarini. Per quanto riguarda i lavori ipertestuali, alle citazioni e/o alle fotografie va sempre aggiunto un link verso la pagina o le pagine del Museo Virtuale o del Museo di Fisica A. M. Traversi utilizzate come fonte. Non copiare totalmente una pagina (testo con o senza foto) o lunghe sezioni; si utilizzino invece link verso le pagine di interesse. La riproduzione di qualsiasi fotografia prelevata da questa pagina in riviste scientifiche e/o in elaborati prodotti nell'ambito di progetti di ricerca necessita del permesso da parte della Direzione del Museo Traversi. Tale permesso, di esclusiva pertinenza della Direzione del Museo, viene eventualmente rilasciato dopo presentazione di un'apposita domanda (si consulti al riguardo la voce Ricerca del sito internet del Museo Traversi). Per altre informazioni si consultino le note in materia di copyright. Tutte le informazioni di carattere tecnico legate agli strumenti descritti nel Museo Virtuale sono oggetto di continuo aggiornamento. Sono pertanto possibili non corrispondenze tra pagina in rete e ultimi dati raccolti; gli interessati sono pregati di contattare la Direzione del Museo. | ||
| URL del Museo Virtuale: http://museo.liceofoscarini.it/virtuale/index.html URL del Museo di Fisica "A. M. Traversi": http://museo.liceofoscarini.it; e-mail: museo.atraversi@del@liceofoscarini.it [Rimuovere "del@" per avere l'indirizzo corretto]. |
| Liceo Classico "Marco Foscarini" - Venezia | ||||