
Note sul copyright
Pagina Facebook
Firma anche tu il
REGISTRO VISITATORI
(GUEST BOOK)
| Meccanica - sistemi di leve | ||
|---|---|---|
 Note sul copyright Pagina Facebook Firma anche tu il REGISTRO VISITATORI (GUEST BOOK) |
Supporto teorico | |
| Leve in serie | ||
Una leva può essere collegata in modo opportuno ad altre leve dando vita ad un sistema di leve in serie. Una simile configurazione trova applicazioni in numerosi meccanismi e anche nei rotimi, in quanto ogni singolo ingranaggio è studiabile come un sistema di due leve in serie. Un sitema di leve in serie è un moltiplicatore di forza.
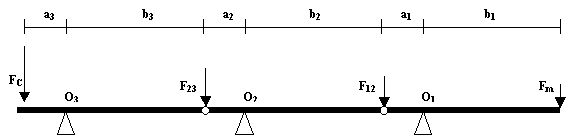
Per provare quanto appena affermato, si consideri il sistema di tre leve in serie disposte come nel disegno qui sopra. In ogni elemento costituente il meccanismo si è indicato con la lettera a il braccio più corto della leva, mentre con la lettera b il braccio più lungo. Per sviluppare la semplice dimostrazione non ci si sofferma sul modo con cui le leve vengono unite tra loro, ma piuttosto sulle forze che si scambiano reciprocamente. La forza F23 è la forza che si scambiano la terza leva con la seconda e ovviamente la forza F12 è la forza che reciprocamente si scambiano la prima leva con la seconda. Infine le forze FC ed Fm possono essere rispettivamente la forza resistente o quella motrice o viceversa a seconda dei casi. In ogni caso esse sono forze esterne al sistema essendo le altre forze interne.
Studiando questo sistema meccanico dal punto di vista statico, è evidente che dalla seconda delle due equazioni cardinali della statica (equilibrio dei momenti) si ricavano le seguenti equazioni: Fma1 = F12b1, F12a2 = F23b2 e F23a3 = FCb3. Effettuando le opportune sostituzioni, alla fine si ricava la relazione FC = Fm(a1a2a3)/(b1b2b3). Poiché ciascun rapporto a/b è minore dell'unità, è evidente che, perché sussista l'equilibrio del sistema, FC dev'essere minore di Fm. La cosa può essere vista nel modo seguente: nel meccanismo la forza FC si accresce nel passaggio da una leva all'altra, come volevasi dimostrare. Così il peso associato ad una massa agganciata all'estremità del braccio b3 è in grado si sostenere il peso prodotto da una massa maggiore agganciata alla fine del braccio a1.
La relazione finale può anche essere scrutta come FC(b1b2b3) = Fm(a1a2a3). Essa dice che il momento ottenuto moltiplicando la forza FC per il braccio dato dal prodotto di tutti i bracci del meccanismo collocati dalla stessa parte (rispetto a ogni fulcro) della forza FC eguaglia il momento ottenuto moltiplicando la forma Fm per il prodotto di tutti gli altri bracci di ogni singola leva ovvero FCb = Fma.
| La riproduzione totale o parziale di questa pagina e/o di sue parti con qualsiasi mezzo è consentita solo se è senza fini di lucro e sempre con la citazione ben visibile su tutti gli oggetti del nome o dei nomi degli autori e del Liceo Marco Foscarini. Per quanto riguarda i lavori ipertestuali, alle citazioni e/o alle fotografie va sempre aggiunto un link verso la pagina o le pagine del Museo Virtuale o del Museo di Fisica A. M. Traversi utilizzate come fonte. Non copiare totalmente una pagina (testo con o senza foto) o lunghe sezioni; si utilizzino invece link verso le pagine di interesse. La riproduzione di qualsiasi fotografia prelevata da questa pagina in riviste scientifiche e/o in elaborati prodotti nell'ambito di progetti di ricerca necessita del permesso da parte della Direzione del Museo Traversi. Tale permesso, di esclusiva pertinenza della Direzione del Museo, viene eventualmente rilasciato dopo presentazione di un'apposita domanda (si consulti al riguardo la voce Ricerca del sito internet del Museo Traversi). Per altre informazioni si consultino le note in materia di copyright. Tutte le informazioni di carattere tecnico legate agli strumenti descritti nel Museo Virtuale sono oggetto di continuo aggiornamento. Sono pertanto possibili non corrispondenze tra pagina in rete e ultimi dati raccolti; gli interessati sono pregati di contattare la Direzione del Museo. | ||
| URL del Museo Virtuale: http://museo.liceofoscarini.it/virtuale/index.html URL del Museo di Fisica "A. M. Traversi": http://museo.liceofoscarini.it; e-mail: museo.atraversi@del@liceofoscarini.it [Rimuovere "del@" per avere l'indirizzo corretto]. |
| Liceo Classico "Marco Foscarini" - Venezia | ||||