
Note sul copyright
Pagina Facebook
Firma anche tu il
REGISTRO VISITATORI
(GUEST BOOK)
 Note sul copyright Pagina Facebook Firma anche tu il REGISTRO VISITATORI (GUEST BOOK) | Elettromagnetismo - Elettrodinamica |
|---|---|
| Supporto teorico | |
| Seconda legge elementare di Laplace |
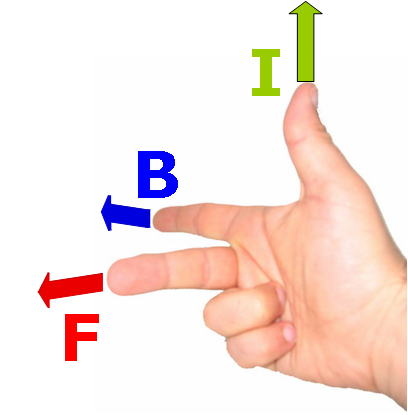 Indicato con il simbolo ds un tratto infinitesimo di filo conduttore che, oltre a trovarsi immerso nel campo magnetico B (grandezza vettoriale), è percorso da una corrente elettrica di intensità I, allora su di esso agisce la forza elementare dF la cui espressione matematica è
Indicato con il simbolo ds un tratto infinitesimo di filo conduttore che, oltre a trovarsi immerso nel campo magnetico B (grandezza vettoriale), è percorso da una corrente elettrica di intensità I, allora su di esso agisce la forza elementare dF la cui espressione matematica è
dF = Ids x B.
In tale relazione, detta seconda legge elementare di Laplace, il simbolo "x" indica il prodotto vettoriale esterno. La direzione e il verso della forza elementare dF si trova facilmente ricorrendo alla regola della mano destra (in questo caso con il pollice che indica il verso di percorrenza della corrente I nel conduttore e l'indice il verso del vettore campo magnetico B).
La forza elementare dF è a tutti gli effetti una forza di Lorentz, poiché la relazione di Lorentz può essere scritta in termini elementari proprio come dF = Ids x B, formula di più immediato utilizzo con i circuiti elettrici e con la quale è possibile giustificare il comportamento (movimenti) di un gran numenro di dispositivi didattici operanti in ambito di elettrodinamica e specificatamente ideati per mettere in evidenza le interazioni tra le correnti e tra le correnti e il campo magnetico. Si vedano, per esempio, le Spirali di Watkins e il Moto rotatorio elettrodinamico.
Per provare quanto appena affermato, il punto di partenza è ricordare che in un conduttore la corrente elettrica è dovuta al movimento dei suoi elettroni sotto l'azione del campo elettrico prodotto dal generatore ad esso applicato (il più delle volte una semplice pila). Per non utlizzare concetti del calcolo infenitesimale, supponiamo che il conduttore, per esempio un pezzo di filo di rame, sia rettilineo e immerso in un campo magnetico uniforme B nello spazio. Su ciascun elettrone che va a costituire la corrente di intensità I, agisce la forza F = qv x B, in cui v è la velocità media di deriva.
Tale forza è trasmessa al conduttore per urto dei portatori di carica con gli ioni del reticolo cristallino. Ne segue che sul tratto di filo, in cui si muovono (Σq) portatori di carica, agisce la forza complessiva F = (Σq)v x B. Così, se il tratto del circuito immerso nel campo magnetico non è vincolato, allora sotto l'azione della forza di Lorentz esso sarà libero di muoversi traslando e/o ruotando (la forza di Lorentz in questo caso produce un momento meccanico).
In un intervallo di tempo t un carica q percorre in media un tratto di filo di lunghezza L=vt; pertanto v=L/t. Dunque si ha
F = (Σq)v x B = (Σq)L/t x B = (Σq/t)L x B = IL x B,
visto che (Σq/t) è la quantità di carica che transita per una sezione trasversale del conduttore nell'unità di tempo, cioè proprio la definizione dell'intensità di corrente I. Se si considera adesso un tratto infinitesimo ds di questo filo, la forza infinitesima che agise su di esso è allora dF = Ids x B, come volevasi dimostrare.
In generale, ovvero in presenza di un tratto finito non rettilineo di filo conduttore percorso da una corrente di intensità I immerso in un campo magnetico non uniforme, il calcolo della forza complessivia F che agisce su di esso utilizzando la seconda legge elementare di Laplace richiede operativamente di sommare tra loro tutti i contributi elementari dF, i quali però non sono punto per punto costanti, essendo B variabile nello spazio e il filo di volta in volta diversamente orientato rispetto al campo magnetico. In matematica questa operazione si chiama integrazione.
| La riproduzione totale o parziale di questa pagina e/o di sue parti con qualsiasi mezzo è consentita solo se è senza fini di lucro e sempre con la citazione ben visibile su tutti gli oggetti del nome o dei nomi degli autori e del Liceo Marco Foscarini. Per quanto riguarda i lavori ipertestuali, alle citazioni e/o alle fotografie va sempre aggiunto un link verso la pagina o le pagine del Museo Virtuale o del Museo di Fisica A. M. Traversi utilizzate come fonte. Non copiare totalmente una pagina (testo con o senza foto) o lunghe sezioni; si utilizzino invece link verso le pagine di interesse. La riproduzione di qualsiasi fotografia prelevata da questa pagina in riviste scientifiche e/o in elaborati prodotti nell'ambito di progetti di ricerca necessita del permesso da parte della Direzione del Museo Traversi. Tale permesso, di esclusiva pertinenza della Direzione del Museo, viene eventualmente rilasciato dopo presentazione di un'apposita domanda (si consulti al riguardo la voce Ricerca del sito internet del Museo Traversi). Per altre informazioni si consultino le note in materia di copyright. Tutte le informazioni di carattere tecnico legate agli strumenti descritti nel Museo Virtuale sono oggetto di continuo aggiornamento. Sono pertanto possibili non corrispondenze tra pagina in rete e ultimi dati raccolti; gli interessati sono pregati di contattare la Direzione del Museo. | ||
| URL del Museo Virtuale: http://museo.liceofoscarini.it/virtuale/index.html URL del Museo di Fisica "A. M. Traversi": http://museo.liceofoscarini.it; e-mail: museo.atraversi@del@liceofoscarini.it [Rimuovere "del@" per avere l'indirizzo corretto]. |
| Liceo Classico "Marco Foscarini" - Venezia | ||||